Hopfield Net
- So far, neural networks for computation are all feedforward structures
Loopy network
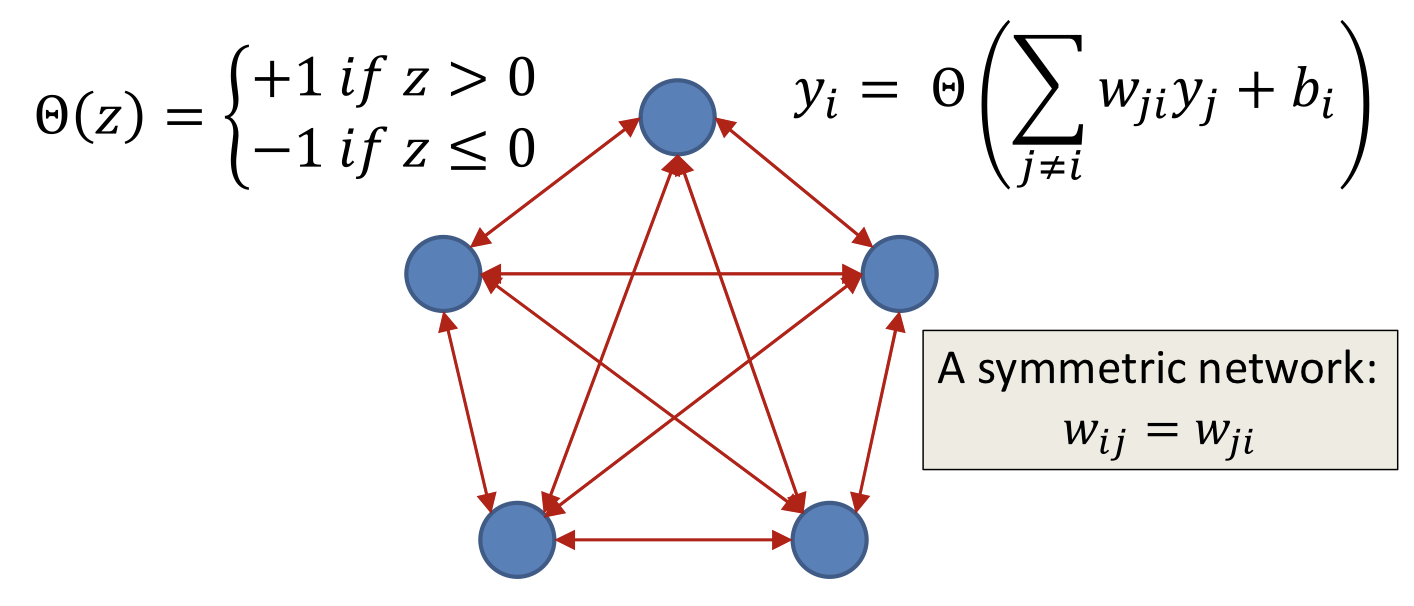
- Each neuron is a perceptron with +1/-1 output
- Every neuron receives input from every other neuron
- Every neuron outputs signals to every other neuron
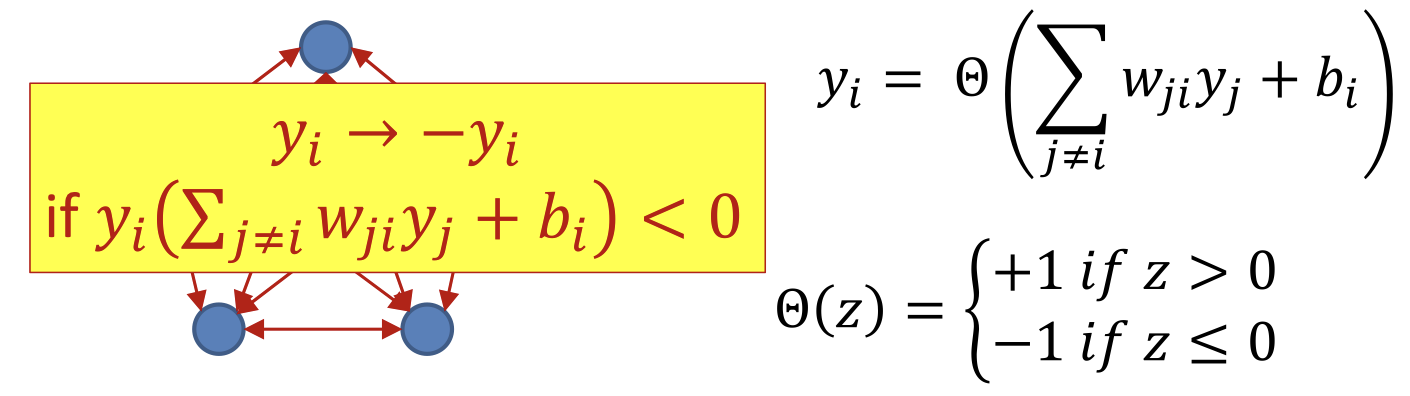
- At each time each neuron receives a “field”
- If the sign of the field matches its own sign, it does not respond
- If the sign of the field opposes its own sign, it “flips” to match the sign of the field
- If the sign of the field at any neuron opposes its own sign, it “flips” to match the field
- Which will change the field at other nodes
- Which may then flip... and so on...
Filp behavior
Let be the output of the -th neuron just before it responds to the current field
Let be the output of the -th neuron just after it responds to the current field
if , then
If the sign of the field matches its own sign, it does not flip
if , then
This term is always positive!
Every flip of a neuron is guaranteed to locally increase
Globally
- Consider the following sum across all nodes
- Assume
- For any unit that “flips” because of the local field
- This is always positive!
- Every flip of a unit results in an increase in
Overall
- Flipping a unit will result in an increase (non-decrease) of
- is bounded
- The minimum increment of in a flip is
- Any sequence of flips must converge in a finite number of steps
- Think of this as an infinite deep network where every weights at every layers are identical
- Find the maximum layer!
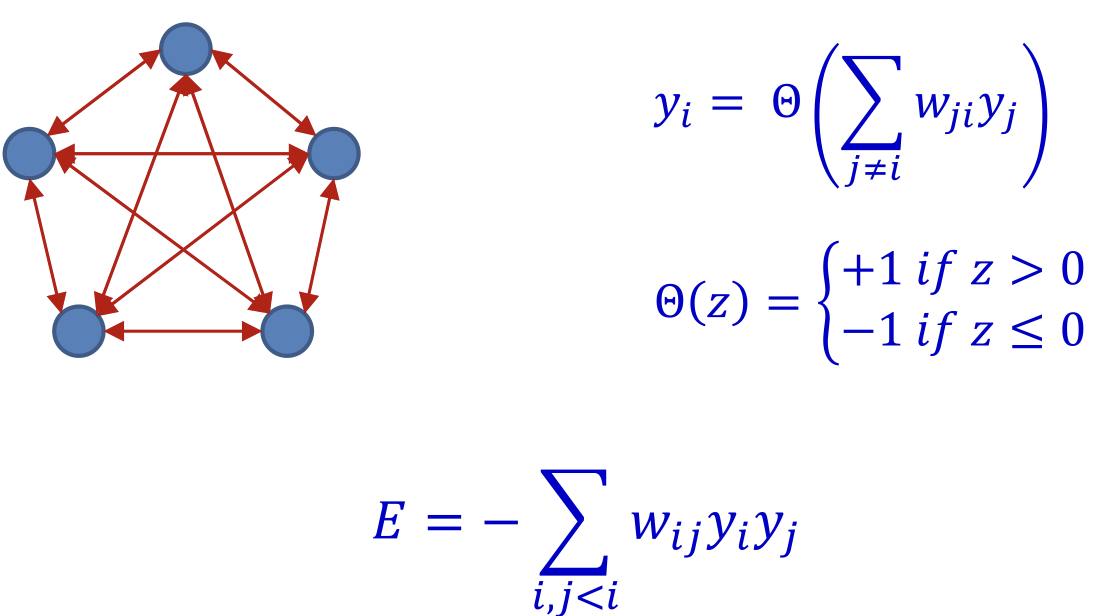
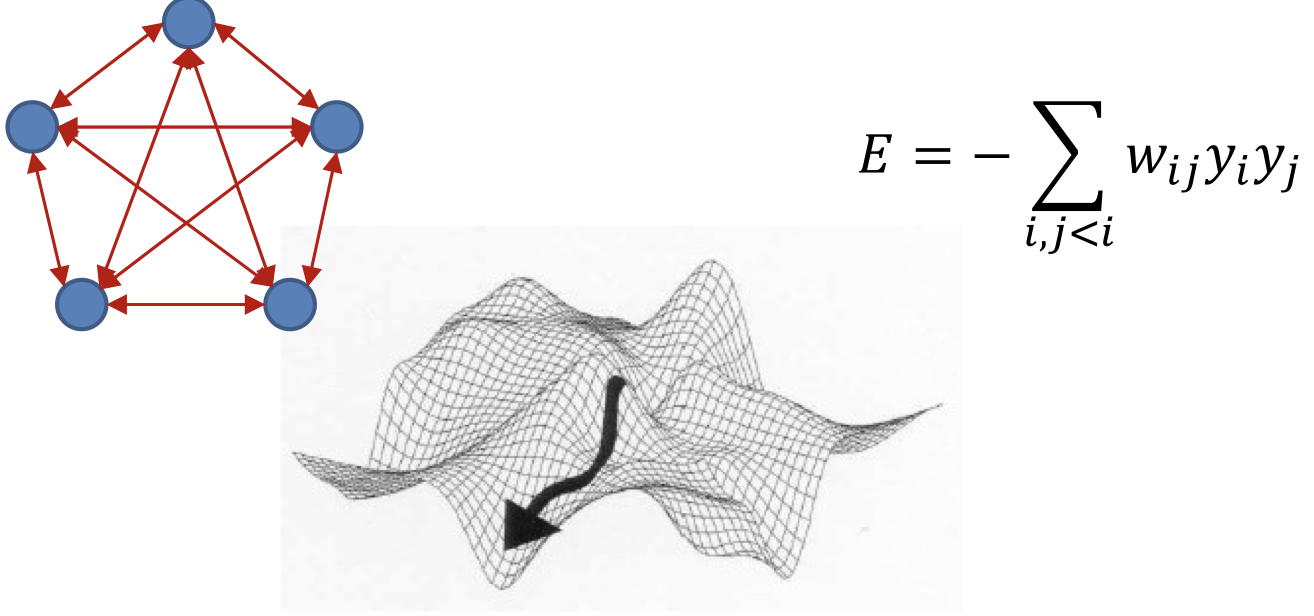
The Energy of a Hopfield Net
- Define the Energy of the network as
- Just the negative of
- The evolution of a Hopfield network constantly decreases its energy
- This is analogous to the potential energy of a spin glass(Magnetic diploes)
- The system will evolve until the energy hits a local minimum
- We remove bias for better understanding
- The network will evolve until it arrives at a local minimum in the energy contour
Content-addressable memory
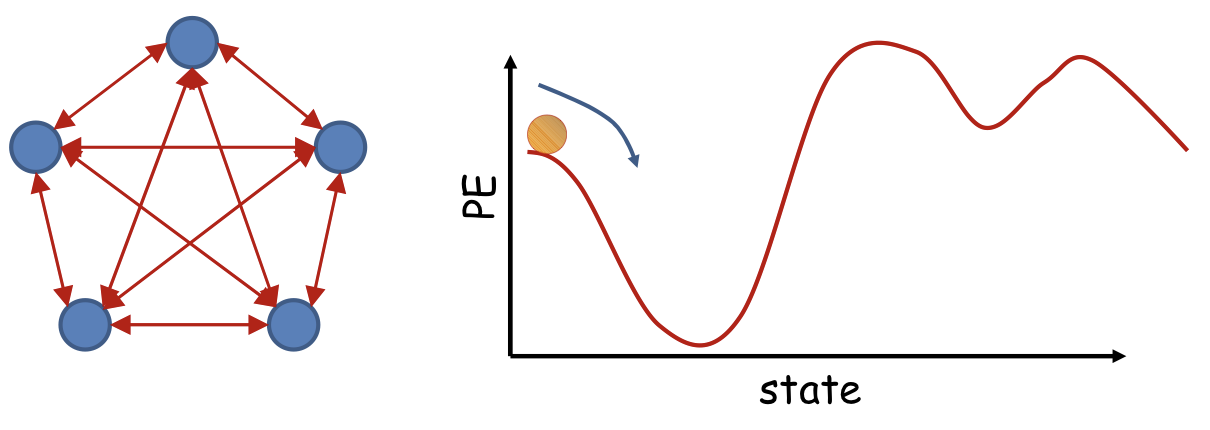
- Each of the minima is a “stored” pattern
- If the network is initialized close to a stored pattern, it will inevitably evolve to the pattern
- This is a content addressable memory
- Recall memory content from partial or corrupt values
- Also called associative memory
- Evolve and recall pattern by content, not by location
Evolution
- The network will evolve until it arrives at a local minimum in the energy contour
- We proved that every change in the network will result in decrease in energy
- So path to energy minimum is monotonic
For 2-neuron net
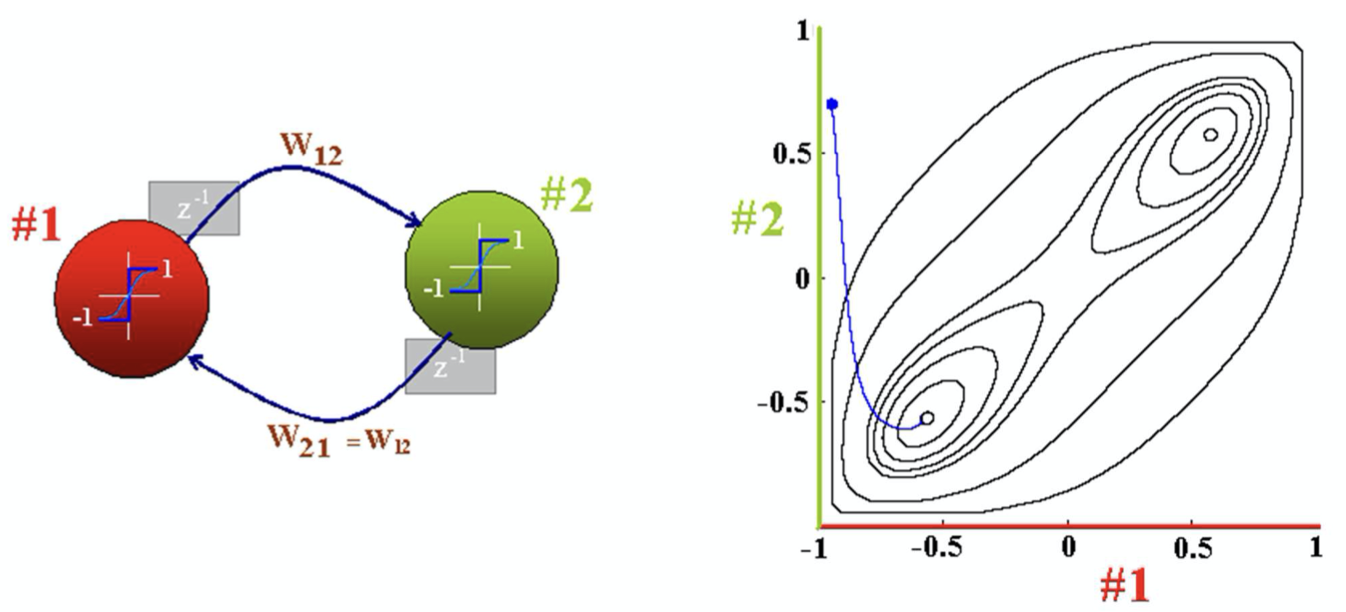
- Symmetric
- If is a local minimum, so is
Computational algorithm

- Very simple
- Updates can be done sequentially, or all at once
- Convergence when it deos not chage significantly any more
Issues
Store a specific pattern
- A network can store multiple patterns
- Every stable point is a stored pattern
- So we could design the net to store multiple patterns
- Remember that every stored pattern is actually two stored patterns, and
- How could the quadrtic function have multiple minimum? (Convex function)
- Input has constrain (belong to )
- Hebbian learning:
- Design a stationary pattern
- So
- Energy
- This is the lowest possible energy value for the network
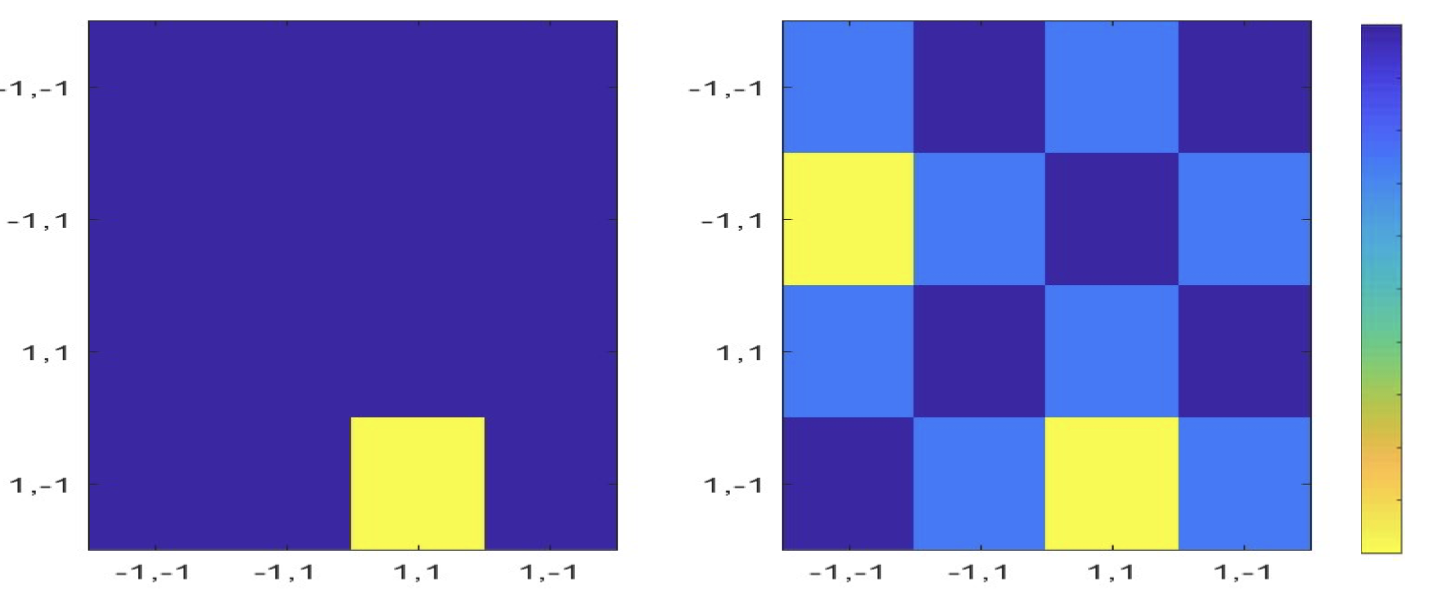
- Stored pattern has lowest energy
- No matter where it begin, it will evolve into yellow pattern(lowest energy)
How many patterns can we store?
- To store more than one pattern
- is the set of patterns to store
- Super/subscript represents the specific pattern
- Hopfield: For a network of neurons can store up to ~ patterns through Hebbian learning(Provided in PPT)
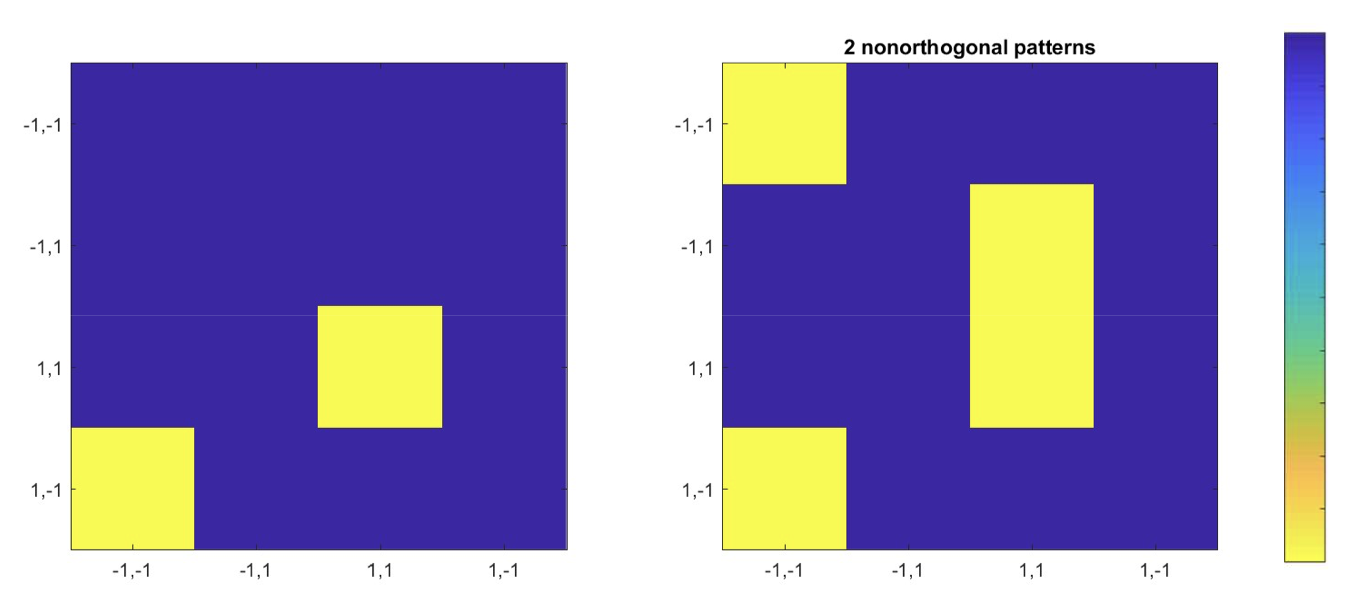
Orthogonal/ Non-orthogonal patterns
Orthogonal patterns

Patterns are local minima (stationary and stable)
- No other local minima exist
- But patterns perfectly confusable for recall
- Non-orthogonal patterns
- Patterns are local minima (stationary and stable)
- No other local minima exist
- Actual wells for patterns
- Patterns may be perfectly recalled! (Note K > 0.14 N)
- No other local minima exist
- Two orthogonal 6-bit patterns
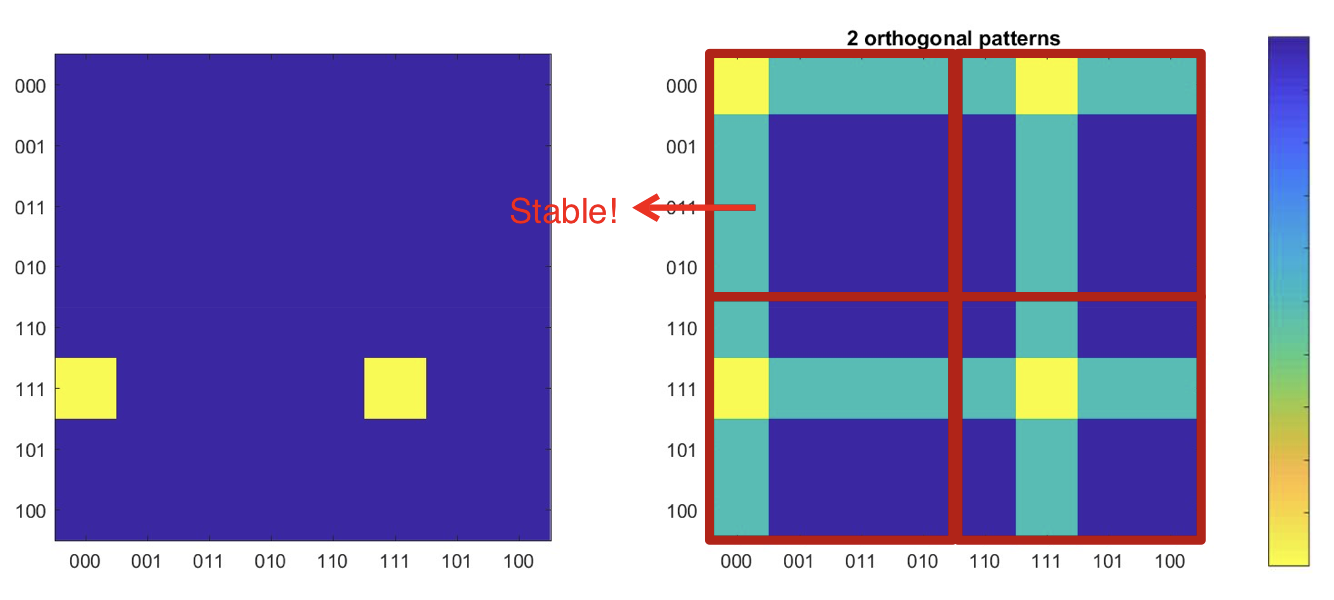
- Perfectly stationary and stable
- Several spurious “fake-memory” local minima..
Observations
- Many “parasitic” patterns
- Undesired patterns that also become stable or attractors
Patterns that are non-orthogonal easier to remember
- I.e. patterns that are closer are easier to remember than patterns that are farther!!
- Seems possible to store K > 0.14N patterns
- i.e. obtain a weight matrix W such that K > 0.14N patterns are stationary
- Possible to make more than 0.14N patterns at-least 1-bit stable